written by: Panagiotis Michalatos and Andrew Payne
Most digital design involves surface modeling. Even so called “solid” modeling software is based on representations where a “solid” is that which is enclosed by a set of boundaries (known as boundary representations or ‘Brep’ for short). While digital representations of solid objects are often treated as homogeneous and discrete entities, the reality is somewhat different. In the real world, material distributions are continuous and varied. Yet, with regard to architectural components, the variability of material within a volume is usually concealed (ie. porosity of bricks, various types of reinforcements for concrete structures, etc.) and is rarely taken into account during the early design process. With the advent of 3d printing techniques, a new possibility emerges - allowing us the ability to reconsider the aesthetic and mechanical properties of visible reinforcement. In this post we discuss a structural optimization method in conjunction with the possibility of treating structural elements as living in a material continuum that renders objects and reinforcements fuzzy.
Topology optimization is a form finding technique which seeks to optimize a certain material distribution with given boundary conditions (ie. types of supports and loads). It departs from standard form finding techniques in that it assumes that a volume of virtual material can continuously vary its stiffness or density throughout space. Until now the final step of this process involved a cut off threshold; a sharp boundary of hard solid material and void. However intermediate steps of topology optimization suggest grey zones of intermediate material stiffness. These results were usually discarded as unrealistic from a fabrication point of view. With multi material printing we can experiment and speculate about possible realizations of such fuzzy structural objects. The analysis and design of the experiments presented here were carried out using the tools Topostruct (a standalone application) and Millipede (a plugin for Grasshopper) created by Panagiotis Michalatos and Sawako Kaijima.
Three experiments were conducted: the first is the design of a chair using standard topology optimization techniques and interpretation (single solid material), the second was a new type of truss/beam element with fuzzy visible reinforcement (soft transparent material encasing gradations of a harder bone-like structure), and the last one was a similar interpretation to the cantilevering slab which produces patterns reminiscent of a leaf (since leaves solve the same structural problem).
Example 1: A chair
The chair example uses topology optimization to gradually remove material from a solid volume on which the actions of a person seating are applied (ie. vertical and horizontal loads for the seating position). 3d printing allows us the ability to materialize the intricate structures that emerge especially around moment connections.
Figure 1: from left to right: Initial boundary volume setup for chair configuration and successive steps of material redistribution through topology optimization. Darker areas designate denser material.
Figure 2: Features of the chair become more refined during each subsequent step through the topology optimization process.
Figures 3 & 4: Converged geometry of the topology optimization process.
Example 2: A fuzzy truss
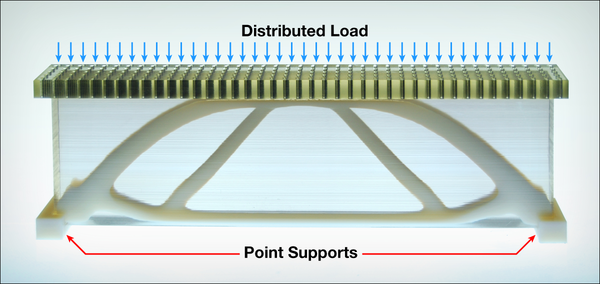
For the second experiment we revisited one of the simplest forms from engineering textbooks. The truss like structures that act like bridges supporting a distributed load at their two end points. However, in this example, the topology optimization routine was set up in such a way that instead of a solid object, it yielded a continuous variation of material stiffness. Using Objet’s multi-material printing technology, we were able to develop a gradated structure using a transparent rubbery material and a hard white material (and the gradations in between the two) to achieve an outcome that looks, feels, and structurally acts like a fuzzy reinforced structure.
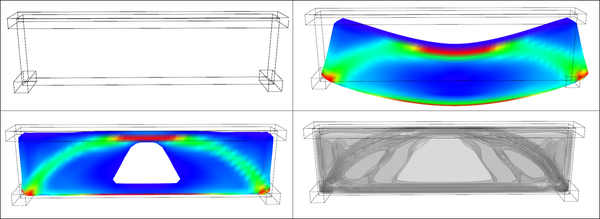
Figure 5: [top left]: Setup of boundary conditions for simple bridge [main volume + supports at the two lower corners and distributed load at the top]. [top right]: Deflected shape of solid material after load application. [bottom images]: stress distribution and topology optimization contours. Inner contours represent regions where stronger material is required.
Figure 6: Topology optimization drives material redistribution within the volume of the truss. A fuzzy truss shaped beam reinforcement gradually emerges.
Figure 7: A 3d printed diagram showing the distributed load on top and the two supports on either end plus the optimal shape of the reinforced region.
Figure 8: Using multi-material printing technology, a fuzzy bone-like structure can be created using gradients between a transparent rubbery material and an opaque hard material. In this way the actual outcome of the topology optimization process can be directly materialized.
Example 3: A leaf-slab
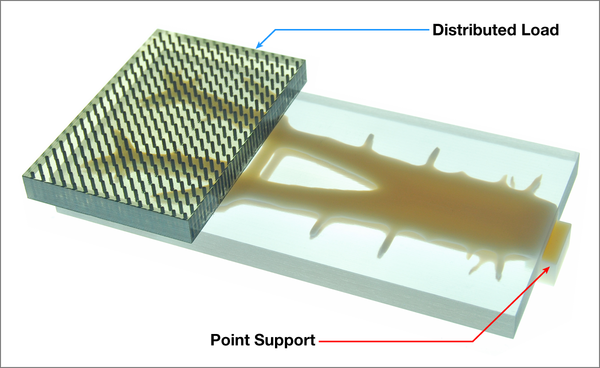
Our final experiment involved the reinterpretation of a different traditional system - the cantilevering slab. The distributed load over this horizontal plate puts similar requirement to that of a leaf and topology optimization yields branching structures reminiscent of the venation found in leaves.
Figure 9: A fuzzy branching pattern emerges when a distributed load is applied to a cantilevering slab from a single support, resembling the vein patterns of leaves.
Figure 10: A 3d printed diagram showing the cantilevered load and support structure.
Figure 11: Multi-material printing allows us to materialize semi-rigid and semi-transparent fuzzy structural systems as a kind of gradual reinforcement embedded in the material where the boundaries between softer and harder parts are blurred.
The ability to continuously vary the stiffness and transparency of material will allow us to rethink design techniques and technologies, software tools, and analysis methods beyond the surface modeling paradigm. In the scale of product design this is already possible thanks to technologies like multi-material 3d printing. Such experiments will be valuable precedents when speculating about new types of continuous and fuzzy building systems.
This research was generously supported by Objet Technologies. For more information about their 3d printing technology, visit http://www.objet.com.